Lessons
 The most unexpected answer to a counting puzzle
A puzzle involving colliding blocks where the number pi, vey unexpectedly, shows up.
Jan 13, 2019
The most unexpected answer to a counting puzzle
A puzzle involving colliding blocks where the number pi, vey unexpectedly, shows up.
Jan 13, 2019
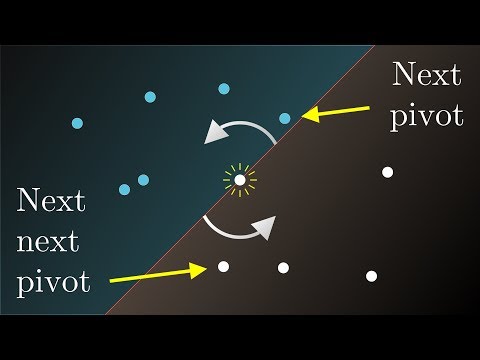 The unexpectedly hard windmill question (2011 IMO, Q2)
Problem 2 from the 2011 IMO
Aug 4, 2019
The unexpectedly hard windmill question (2011 IMO, Q2)
Problem 2 from the 2011 IMO
Aug 4, 2019
 Who cares about topology? (Inscribed rectangle problem)
This is an absolutely beautiful piece of math. It shows how certain ideas from topology, such as the mobius strip, can be used to solve a slightly softer form of an unsolved problem in geometry.
Nov 4, 2016
Who cares about topology? (Inscribed rectangle problem)
This is an absolutely beautiful piece of math. It shows how certain ideas from topology, such as the mobius strip, can be used to solve a slightly softer form of an unsolved problem in geometry.
Nov 4, 2016
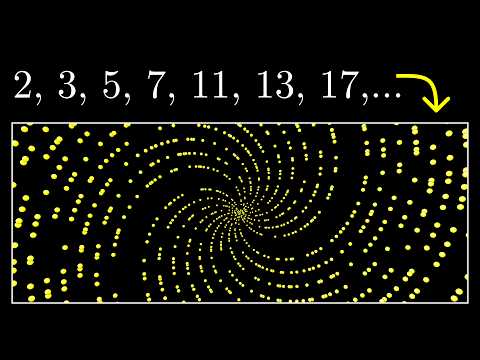 Why do prime numbers make these spirals?
A curious pattern in polar plots with prime numbers, together with discussion of Dirichlet's theorem
Oct 8, 2019
Why do prime numbers make these spirals?
A curious pattern in polar plots with prime numbers, together with discussion of Dirichlet's theorem
Oct 8, 2019
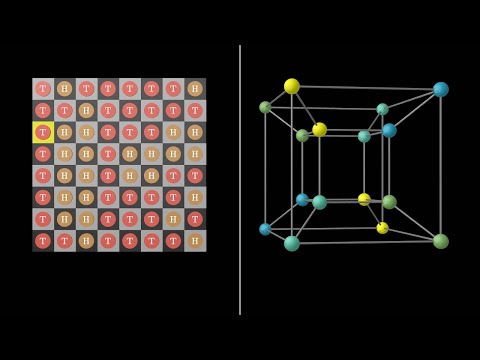 The impossible chessboard puzzle
An information puzzle with an interesting twist
Jul 5, 2020
The impossible chessboard puzzle
An information puzzle with an interesting twist
Jul 5, 2020
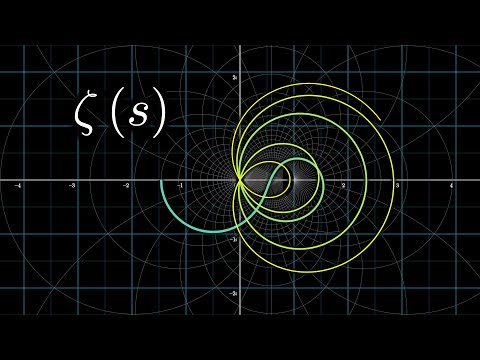 Visualizing the Riemann zeta function and analytic continuation
What is the Riemann zeta function? What is analytic continuation? This video lays out the complex analysis needed to answer these questions.
Dec 9, 2016
Visualizing the Riemann zeta function and analytic continuation
What is the Riemann zeta function? What is analytic continuation? This video lays out the complex analysis needed to answer these questions.
Dec 9, 2016
 The Brachistochrone, with Steven Strogatz
A classic problem that Johann Bernoulli posed to famous mathematicians of his time, such as Newton, and how Bernoulli found an incredibly clever solution using properties of light.
Apr 1, 2016
The Brachistochrone, with Steven Strogatz
A classic problem that Johann Bernoulli posed to famous mathematicians of his time, such as Newton, and how Bernoulli found an incredibly clever solution using properties of light.
Apr 1, 2016
 The Essence of Calculus
An overview of what calculus is all about, with an emphasis on making it seem like something students could discover for themselves. The central example is that of rediscovering the formula for a circle's area, and how this is an isolated instance of the fundamental theorem of calculus
Apr 28, 2017
The Essence of Calculus
An overview of what calculus is all about, with an emphasis on making it seem like something students could discover for themselves. The central example is that of rediscovering the formula for a circle's area, and how this is an isolated instance of the fundamental theorem of calculus
Apr 28, 2017
 The paradox of the derivative
An introduction to what a derivative is, and how it formalizes an otherwise paradoxical idea.
Apr 29, 2017
The paradox of the derivative
An introduction to what a derivative is, and how it formalizes an otherwise paradoxical idea.
Apr 29, 2017
 Derivative formulas through geometry
Introduction to the derivatives of polynomial terms and trigonometric functions thought about geometrically and intuitively. The goal is for these formulas to feel like something the student could have discovered, rather than something to be memorized.
Apr 30, 2017
Derivative formulas through geometry
Introduction to the derivatives of polynomial terms and trigonometric functions thought about geometrically and intuitively. The goal is for these formulas to feel like something the student could have discovered, rather than something to be memorized.
Apr 30, 2017
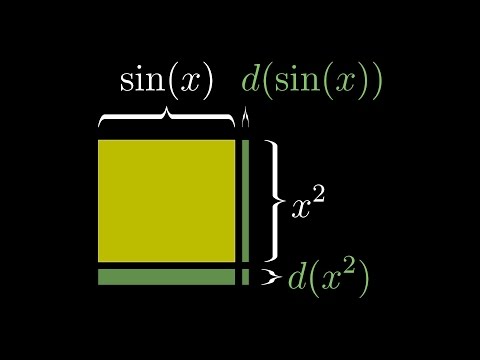 Visualizing the chain rule and product rule
The product rule and chain rule in calculus can feel like they were pulled out of thin air, but is there an intuitive way to think about them?
May 1, 2017
Visualizing the chain rule and product rule
The product rule and chain rule in calculus can feel like they were pulled out of thin air, but is there an intuitive way to think about them?
May 1, 2017
 What's so special about Euler's number e?
What is the derivative of a^x? Why is e^x its own derivative? This video shows how to think about the rule for differentiating exponential functions.
May 2, 2017
What's so special about Euler's number e?
What is the derivative of a^x? Why is e^x its own derivative? This video shows how to think about the rule for differentiating exponential functions.
May 2, 2017
 Implicit differentiation, what's going on here?
How to think about implicit differentiation in terms of functions with multiple inputs, and tiny nudges to those inputs.
May 3, 2017
Implicit differentiation, what's going on here?
How to think about implicit differentiation in terms of functions with multiple inputs, and tiny nudges to those inputs.
May 3, 2017
 Limits, L'Hôpital's rule, and epsilon delta definitions
What are limits? How are they defined? How are they used to define the derivative? What is L'Hospital's rule?
May 4, 2017
Limits, L'Hôpital's rule, and epsilon delta definitions
What are limits? How are they defined? How are they used to define the derivative? What is L'Hospital's rule?
May 4, 2017
 Integration and the fundamental theorem of calculus
What is integration? Why is it computed as the opposite of differentiation? What is the fundamental theorem of calculus?
May 5, 2017
Integration and the fundamental theorem of calculus
What is integration? Why is it computed as the opposite of differentiation? What is the fundamental theorem of calculus?
May 5, 2017
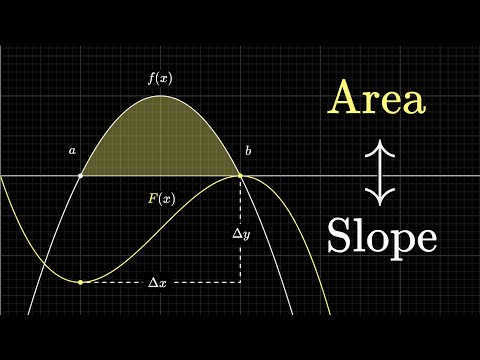 What does area have to do with slope?
Derivatives are about slope, and integration is about area. These ideas seem completely different, so why are they inverses?
May 6, 2017
What does area have to do with slope?
Derivatives are about slope, and integration is about area. These ideas seem completely different, so why are they inverses?
May 6, 2017
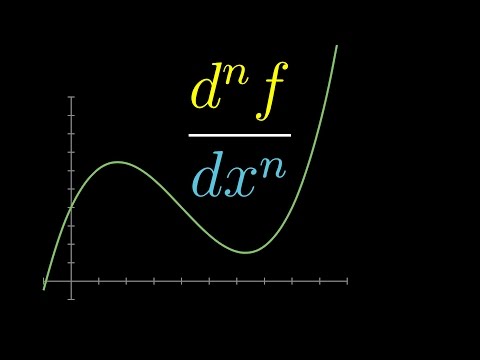 Higher order derivatives
What is the second derivative? Third derivative? How do you think about these?
May 7, 2017
Higher order derivatives
What is the second derivative? Third derivative? How do you think about these?
May 7, 2017
 Taylor series
Taylor series are extremely useful in engineering and math, but what are they? This video shows why they're useful, and how to make sense of the formula.
May 7, 2017
Taylor series
Taylor series are extremely useful in engineering and math, but what are they? This video shows why they're useful, and how to make sense of the formula.
May 7, 2017
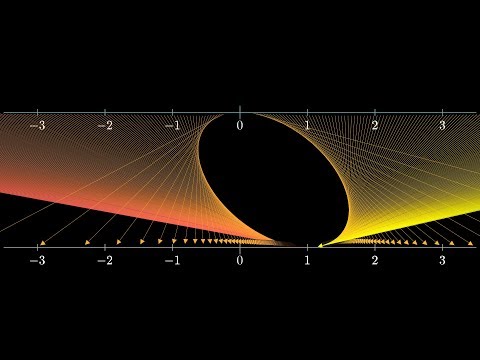 The other way to visualize derivatives
A visual for derivatives which generalizes more nicely to topics beyond calculus. Thinking of a function as a transformation, the derivative measure how much that function locally stretches or squishes a given region.
May 19, 2018
The other way to visualize derivatives
A visual for derivatives which generalizes more nicely to topics beyond calculus. Thinking of a function as a transformation, the derivative measure how much that function locally stretches or squishes a given region.
May 19, 2018
 Essence of linear algebra preview
The introduction to a series on visualizing core ideas of linear algebra.
Aug 5, 2016
Essence of linear algebra preview
The introduction to a series on visualizing core ideas of linear algebra.
Aug 5, 2016
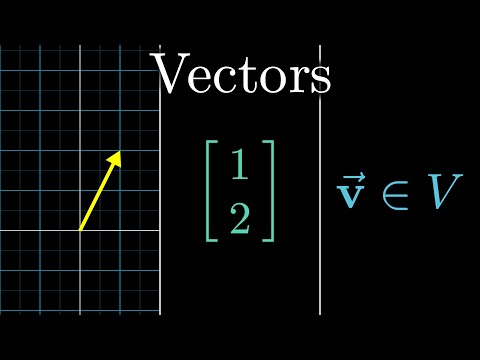 Vectors, what even are they?
What is a vector? Is it an arrow in space? A list of numbers?
Aug 6, 2016
Vectors, what even are they?
What is a vector? Is it an arrow in space? A list of numbers?
Aug 6, 2016
 Linear combinations, span, and basis vectors
Some foundational ideas in linear algebra: Span, linear combinations, and linear dependence.
Aug 6, 2016
Linear combinations, span, and basis vectors
Some foundational ideas in linear algebra: Span, linear combinations, and linear dependence.
Aug 6, 2016
 Linear transformations and matrices
When you think of matrices as transforming space, rather than as grids of numbers, so much of linear algebra starts to make sense.
Aug 7, 2016
Linear transformations and matrices
When you think of matrices as transforming space, rather than as grids of numbers, so much of linear algebra starts to make sense.
Aug 7, 2016
 Matrix multiplication as composition
How to think about matrix multiplication visually as successively applying two different linear transformations.
Aug 8, 2016
Matrix multiplication as composition
How to think about matrix multiplication visually as successively applying two different linear transformations.
Aug 8, 2016
 Three-dimensional linear transformations
How to think of 3x3 matrices as transforming 3d space
Aug 9, 2016
Three-dimensional linear transformations
How to think of 3x3 matrices as transforming 3d space
Aug 9, 2016
 The determinant
The determinant has a very natural visual intuition, even though it's formula can make it seem more complicated than it really is.
Aug 10, 2016
The determinant
The determinant has a very natural visual intuition, even though it's formula can make it seem more complicated than it really is.
Aug 10, 2016
 Inverse matrices, column space and null space
How do you think about the column space and null space of a matrix visually? How do you think about the inverse of a matrix?
Aug 15, 2016
Inverse matrices, column space and null space
How do you think about the column space and null space of a matrix visually? How do you think about the inverse of a matrix?
Aug 15, 2016
 Nonsquare matrices as transformations between dimensions
How do you think about a non-square matrix as a transformation?
Aug 16, 2016
Nonsquare matrices as transformations between dimensions
How do you think about a non-square matrix as a transformation?
Aug 16, 2016
 Dot products and duality
What is the dot product? What does it represent? Why does it have the formula that it does? All this is explained visually.
Aug 24, 2016
Dot products and duality
What is the dot product? What does it represent? Why does it have the formula that it does? All this is explained visually.
Aug 24, 2016
 Cross products
The cross product is a way to multiple to vectors in 3d. This video shows how to visualize what it means.
Sep 1, 2016
Cross products
The cross product is a way to multiple to vectors in 3d. This video shows how to visualize what it means.
Sep 1, 2016
 Cross products in the light of linear transformations
The formula for the cross product can feel like a mystery, or some kind of crazy coincidence. But it isn't. There is a fundamental connection between the cross product and determinants.
Sep 1, 2016
Cross products in the light of linear transformations
The formula for the cross product can feel like a mystery, or some kind of crazy coincidence. But it isn't. There is a fundamental connection between the cross product and determinants.
Sep 1, 2016
 Cramer's rule, explained geometrically
What Cramer's rule is, and a geometric reason it's true
Mar 17, 2019
Cramer's rule, explained geometrically
What Cramer's rule is, and a geometric reason it's true
Mar 17, 2019
 Change of basis
What is a change of basis, and how do you do it?
Sep 11, 2016
Change of basis
What is a change of basis, and how do you do it?
Sep 11, 2016
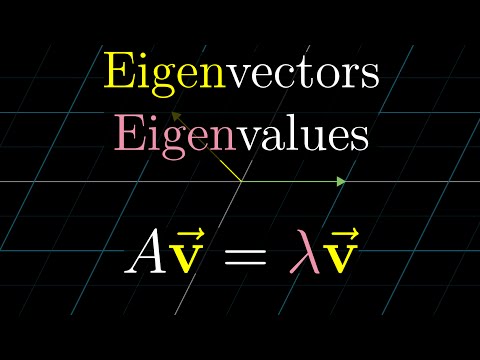 Eigenvectors and eigenvalues
Eigenvalues and eigenvectors are one of the most important ideas in linear algebra, but what on earth are they?
Sep 15, 2016
Eigenvectors and eigenvalues
Eigenvalues and eigenvectors are one of the most important ideas in linear algebra, but what on earth are they?
Sep 15, 2016
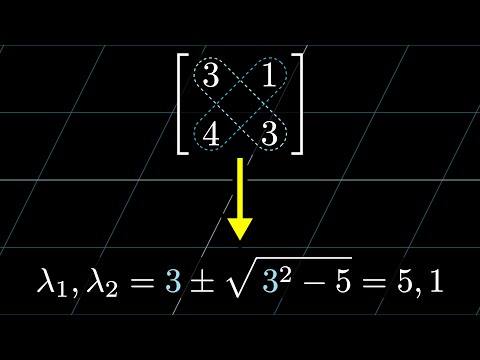 A quick trick for computing eigenvalues
A quick way to compute eigenvalues of a 2x2 matrix
May 7, 2021
A quick trick for computing eigenvalues
A quick way to compute eigenvalues of a 2x2 matrix
May 7, 2021
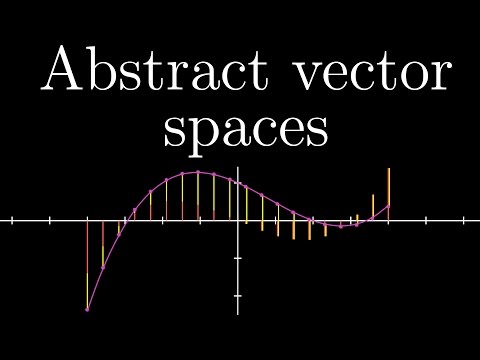 Abstract vector spaces
What is a vector space? Even though they are initial taught in the context of arrows in space, or with vectors being lists of numbers, the idea is much more general and far-reaching.
Sep 24, 2016
Abstract vector spaces
What is a vector space? Even though they are initial taught in the context of arrows in space, or with vectors being lists of numbers, the idea is much more general and far-reaching.
Sep 24, 2016
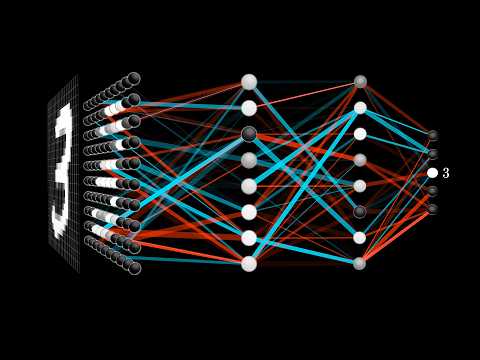 But what is a Neural Network?
An overview of what a neural network is, introduced in the context of recognizing hand-written digits.
Oct 5, 2017
But what is a Neural Network?
An overview of what a neural network is, introduced in the context of recognizing hand-written digits.
Oct 5, 2017
 Gradient descent, how neural networks learn
An overview of gradient descent in the context of neural networks. This is a method used widely throughout machine learning for optimizing how a computer performs on certain tasks.
Oct 16, 2017
Gradient descent, how neural networks learn
An overview of gradient descent in the context of neural networks. This is a method used widely throughout machine learning for optimizing how a computer performs on certain tasks.
Oct 16, 2017
 What is backpropagation really doing?
An overview of backpropagation, the algorithm behind how neural networks learn.
Nov 3, 2017
What is backpropagation really doing?
An overview of backpropagation, the algorithm behind how neural networks learn.
Nov 3, 2017
 Backpropagation calculus
The math of backpropagation, the algorithm by which neural networks learn.
Nov 3, 2017
Backpropagation calculus
The math of backpropagation, the algorithm by which neural networks learn.
Nov 3, 2017
 Differential equations, studying the unsolvable | DE1
What is a differential equation, the pendulum equation, and some basic numerical methods
Mar 31, 2019
Differential equations, studying the unsolvable | DE1
What is a differential equation, the pendulum equation, and some basic numerical methods
Mar 31, 2019
 But what is a partial differential equation? | DE2
The heat equation, as an introductory PDE.
Apr 21, 2019
But what is a partial differential equation? | DE2
The heat equation, as an introductory PDE.
Apr 21, 2019
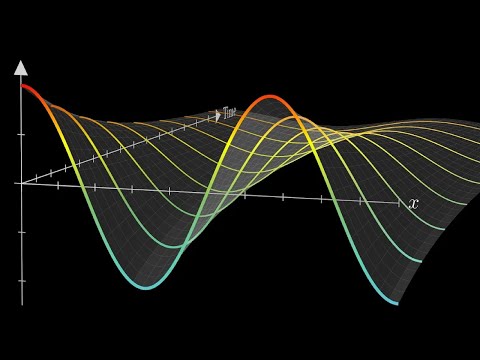 Solving the heat equation | DE3
Solving the heat equation.
Jun 16, 2019
Solving the heat equation | DE3
Solving the heat equation.
Jun 16, 2019
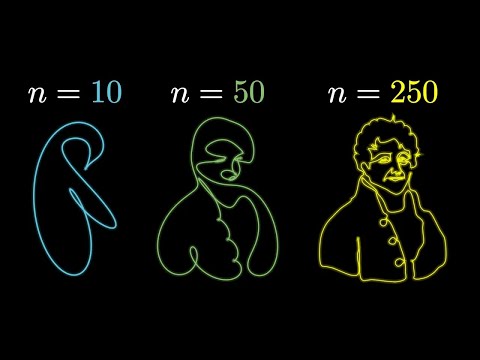 But what is a Fourier series? From heat flow to circle drawings | DE4
Fourier series, from the heat equation to sines to cycles.
Jun 30, 2019
But what is a Fourier series? From heat flow to circle drawings | DE4
Fourier series, from the heat equation to sines to cycles.
Jun 30, 2019
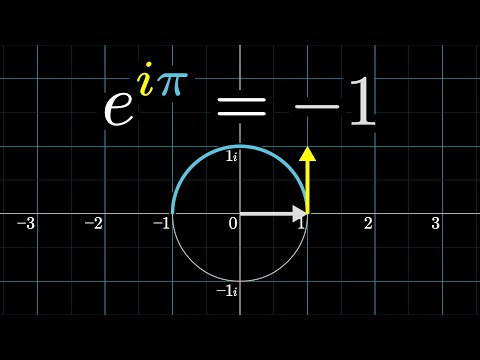 e^(iπ) in 3.14 minutes, using dynamics | DE5
A quick explanation of e^(pi i) in terms of motion and differential equations
Jul 7, 2019
e^(iπ) in 3.14 minutes, using dynamics | DE5
A quick explanation of e^(pi i) in terms of motion and differential equations
Jul 7, 2019
 How (and why) to raise e to the power of a matrix | DE6
Exponentiating matrices, and the kinds of linear differential equations this solves.
Apr 1, 2021
How (and why) to raise e to the power of a matrix | DE6
Exponentiating matrices, and the kinds of linear differential equations this solves.
Apr 1, 2021
 Who cares about topology? (Inscribed rectangle problem)
This is an absolutely beautiful piece of math. It shows how certain ideas from topology, such as the mobius strip, can be used to solve a slightly softer form of an unsolved problem in geometry.
Nov 4, 2016
Who cares about topology? (Inscribed rectangle problem)
This is an absolutely beautiful piece of math. It shows how certain ideas from topology, such as the mobius strip, can be used to solve a slightly softer form of an unsolved problem in geometry.
Nov 4, 2016
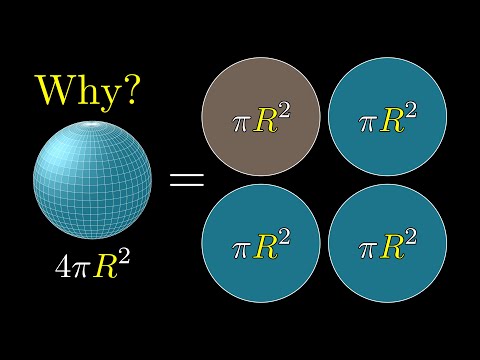 But why is a sphere's surface area four times its shadow?
Two proofs for the surface area of a sphere
Dec 2, 2018
But why is a sphere's surface area four times its shadow?
Two proofs for the surface area of a sphere
Dec 2, 2018
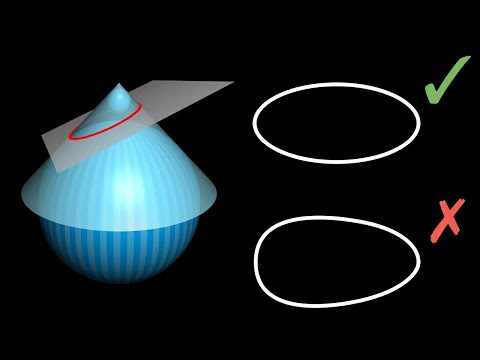 Why slicing a cone gives an ellipse
A beautiful proof of why slicing a cone gives an ellipse.
Aug 1, 2018
Why slicing a cone gives an ellipse
A beautiful proof of why slicing a cone gives an ellipse.
Aug 1, 2018
 Sneaky Topology | The Borsuk-Ulam theorem and stolen necklaces
Solving a discrete math puzzle, namely the stolen necklace problem, using topology, namely the Borsuk Ulam theorem
Nov 18, 2018
Sneaky Topology | The Borsuk-Ulam theorem and stolen necklaces
Solving a discrete math puzzle, namely the stolen necklace problem, using topology, namely the Borsuk Ulam theorem
Nov 18, 2018
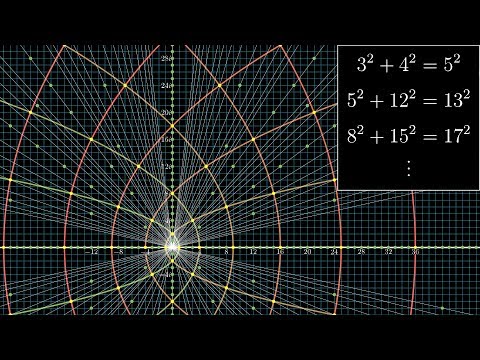 All possible pythagorean triples, visualized
There are a few special right triangles many of us learn about in school, like the 3-4-5 triangle or the 5-12-13 triangle. Is there a way to understand all triplets of numbers (a, b, c) that satisfy a^2 + b^2 = c^2? There is! And it uses complex numbers in a clever way.
May 26, 2017
All possible pythagorean triples, visualized
There are a few special right triangles many of us learn about in school, like the 3-4-5 triangle or the 5-12-13 triangle. Is there a way to understand all triplets of numbers (a, b, c) that satisfy a^2 + b^2 = c^2? There is! And it uses complex numbers in a clever way.
May 26, 2017
 Winding numbers and domain coloring
An algorithm for solving continuous 2d equations using winding numbers.
Mar 24, 2018
Winding numbers and domain coloring
An algorithm for solving continuous 2d equations using winding numbers.
Mar 24, 2018
 Binary, Hanoi and Sierpinski, part 1
How couting in binary can solve the famous tower's of hanoi problem.
Nov 25, 2016
Binary, Hanoi and Sierpinski, part 1
How couting in binary can solve the famous tower's of hanoi problem.
Nov 25, 2016
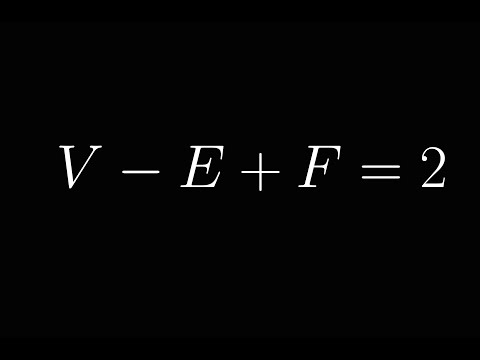 Euler's Formula and Graph Duality
A very clever proof of Euler's characteristic formula using spanning trees.
Jun 21, 2015
Euler's Formula and Graph Duality
A very clever proof of Euler's characteristic formula using spanning trees.
Jun 21, 2015
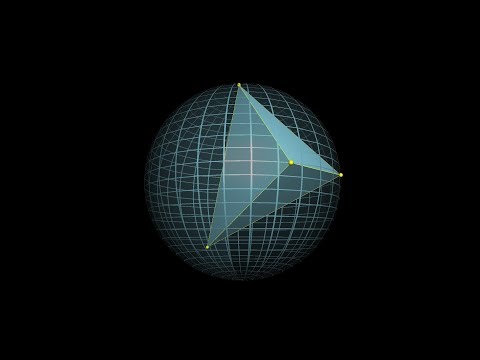 The hardest problem on the hardest test
A geometry/probability question on the Putnam, a famously hard test, about a random tetrahedron in a sphere. This offers an opportunity not just for a lesson about the problem, but about problem-solving tactics in general.
Dec 8, 2017
The hardest problem on the hardest test
A geometry/probability question on the Putnam, a famously hard test, about a random tetrahedron in a sphere. This offers an opportunity not just for a lesson about the problem, but about problem-solving tactics in general.
Dec 8, 2017
 The unexpectedly hard windmill question (2011 IMO, Q2)
Problem 2 from the 2011 IMO
Aug 4, 2019
The unexpectedly hard windmill question (2011 IMO, Q2)
Problem 2 from the 2011 IMO
Aug 4, 2019
 Why do prime numbers make these spirals?
A curious pattern in polar plots with prime numbers, together with discussion of Dirichlet's theorem
Oct 8, 2019
Why do prime numbers make these spirals?
A curious pattern in polar plots with prime numbers, together with discussion of Dirichlet's theorem
Oct 8, 2019
 The impossible chessboard puzzle
An information puzzle with an interesting twist
Jul 5, 2020
The impossible chessboard puzzle
An information puzzle with an interesting twist
Jul 5, 2020
 Circle Division Solution
Moser's circle problem, and its solution.
May 24, 2015
Circle Division Solution
Moser's circle problem, and its solution.
May 24, 2015
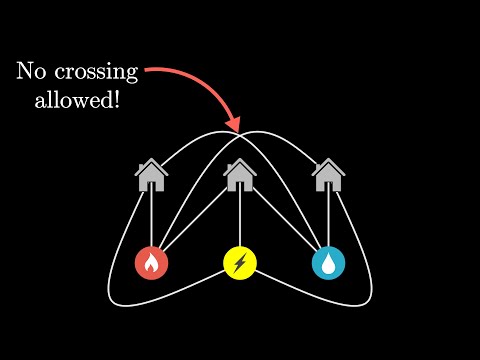 The three utilities puzzle with math/science YouTubers
A classic puzzle in graph theory, the "Utilities problem", a description of why it is unsolvable on a plane, and how it becomes solvable on surfaces with a different topology.
Dec 23, 2017
The three utilities puzzle with math/science YouTubers
A classic puzzle in graph theory, the "Utilities problem", a description of why it is unsolvable on a plane, and how it becomes solvable on surfaces with a different topology.
Dec 23, 2017
 The most unexpected answer to a counting puzzle
A puzzle involving colliding blocks where the number pi, vey unexpectedly, shows up.
Jan 13, 2019
The most unexpected answer to a counting puzzle
A puzzle involving colliding blocks where the number pi, vey unexpectedly, shows up.
Jan 13, 2019
 Why do colliding blocks compute pi?
A solution to the puzzle involving two blocks, sliding fricionlessly, where the number of collisions mysteriously computes pi
Jan 20, 2019
Why do colliding blocks compute pi?
A solution to the puzzle involving two blocks, sliding fricionlessly, where the number of collisions mysteriously computes pi
Jan 20, 2019
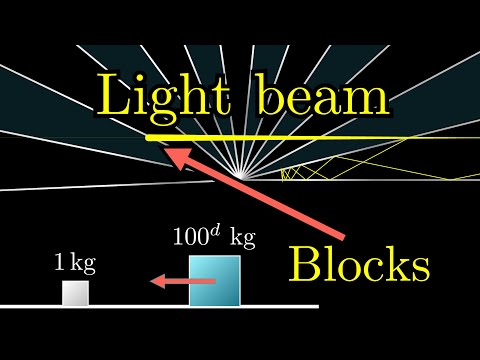 How colliding blocks act like a beam of light...to compute pi.
The third and final part of the block collision sequence.
Feb 3, 2019
How colliding blocks act like a beam of light...to compute pi.
The third and final part of the block collision sequence.
Feb 3, 2019
 Why is pi here? And why is it squared? A geometric answer to the Basel problem
A beautiful solution to the Basel Problem (1+1/4+1/9+1/16+...) using Euclidian geometry. Unlike many more common proofs, this one makes it very clear why pi is involved in the answer.
Mar 2, 2018
Why is pi here? And why is it squared? A geometric answer to the Basel problem
A beautiful solution to the Basel Problem (1+1/4+1/9+1/16+...) using Euclidian geometry. Unlike many more common proofs, this one makes it very clear why pi is involved in the answer.
Mar 2, 2018
 Pi hiding in prime regularities
A beutiful derivation of a formula for pi. At first, 1-1/3+1/5-1/7+1/9-.... seems unrelated to circles, but in fact there is a circle hiding here, as well as some interesting facts about prime numbers in the context of complex numbers.
May 19, 2017
Pi hiding in prime regularities
A beutiful derivation of a formula for pi. At first, 1-1/3+1/5-1/7+1/9-.... seems unrelated to circles, but in fact there is a circle hiding here, as well as some interesting facts about prime numbers in the context of complex numbers.
May 19, 2017
 The Wallis product for pi, proved geometrically
A proof of the Wallis product for pi, together with some neat tricks using complex numbers to analyze circle geometry.
Apr 20, 2018
The Wallis product for pi, proved geometrically
A proof of the Wallis product for pi, together with some neat tricks using complex numbers to analyze circle geometry.
Apr 20, 2018
 How pi was almost 6.283185...
A bit of the history behind how we came to use the symbol "pi" to represent what it does today, and how Euler used it to refer to several different circle constants.
Mar 14, 2018
How pi was almost 6.283185...
A bit of the history behind how we came to use the symbol "pi" to represent what it does today, and how Euler used it to refer to several different circle constants.
Mar 14, 2018
 But what is the Fourier Transform? A visual introduction.
An animated introduction to the Fourier Transform, winding graphs around circles.
Jan 26, 2018
But what is the Fourier Transform? A visual introduction.
An animated introduction to the Fourier Transform, winding graphs around circles.
Jan 26, 2018
 The more general uncertainty principle, beyond quantum
The general uncertainty principle, about the concentration of a wave vs the concentration of its fourier transform, applied to two non-quantum examples before showing what it means for the Heisenberg uncertainty principle.
Feb 25, 2018
The more general uncertainty principle, beyond quantum
The general uncertainty principle, about the concentration of a wave vs the concentration of its fourier transform, applied to two non-quantum examples before showing what it means for the Heisenberg uncertainty principle.
Feb 25, 2018
 Visualizing the Riemann zeta function and analytic continuation
What is the Riemann zeta function? What is analytic continuation? This video lays out the complex analysis needed to answer these questions.
Dec 9, 2016
Visualizing the Riemann zeta function and analytic continuation
What is the Riemann zeta function? What is analytic continuation? This video lays out the complex analysis needed to answer these questions.
Dec 9, 2016
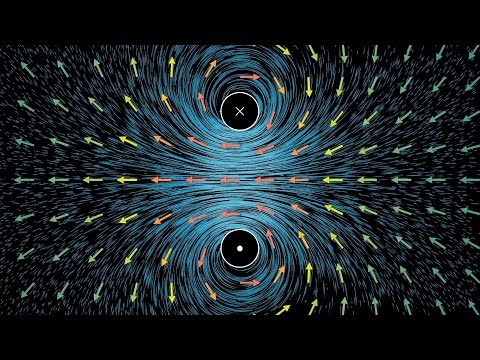 Divergence and curl: The language of Maxwell's equations, fluid flow, and more
Divergence, curl, and their relation to fluid flow and electromagnetism
Jun 21, 2018
Divergence and curl: The language of Maxwell's equations, fluid flow, and more
Divergence, curl, and their relation to fluid flow and electromagnetism
Jun 21, 2018
 Hilbert's Curve: Is infinite math useful?
Drawing curves that fill all of space, and a philosophical take on why mathematics about infinite objects can still be useful in finite contexts.
Jul 21, 2017
Hilbert's Curve: Is infinite math useful?
Drawing curves that fill all of space, and a philosophical take on why mathematics about infinite objects can still be useful in finite contexts.
Jul 21, 2017
 Fractals are typically not self-similar
What exactly are fractals? A common misconception is that they are shapes which look exactly like themselves when you zoom in. In fact, the definition has something to do with the idea of "fractal dimension".
Jan 27, 2017
Fractals are typically not self-similar
What exactly are fractals? A common misconception is that they are shapes which look exactly like themselves when you zoom in. In fact, the definition has something to do with the idea of "fractal dimension".
Jan 27, 2017
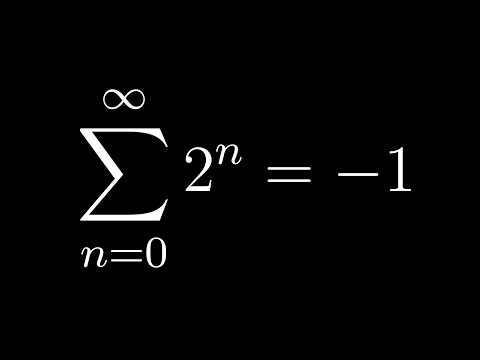 What does it feel like to invent math?
A journey through infinite sums, p-adic numbers, and what it feels like to invent new math.
Aug 14, 2015
What does it feel like to invent math?
A journey through infinite sums, p-adic numbers, and what it feels like to invent new math.
Aug 14, 2015
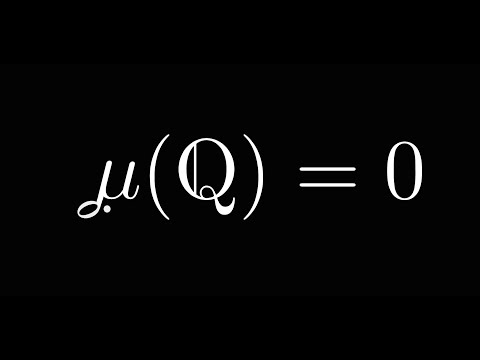 Music And Measure Theory
How one of the introductory ideas in a field called "measure theory" can be thought of in terms of musical harnomy and dissonance.
Oct 4, 2015
Music And Measure Theory
How one of the introductory ideas in a field called "measure theory" can be thought of in terms of musical harnomy and dissonance.
Oct 4, 2015
 Hamming codes and error correction
A discovery-oriented introduction to error correction codes.
Sep 4, 2020
Hamming codes and error correction
A discovery-oriented introduction to error correction codes.
Sep 4, 2020
 Hamming codes part 2, the elegance of it all
How to implement Hamming Codes with xors
Sep 4, 2020
Hamming codes part 2, the elegance of it all
How to implement Hamming Codes with xors
Sep 4, 2020
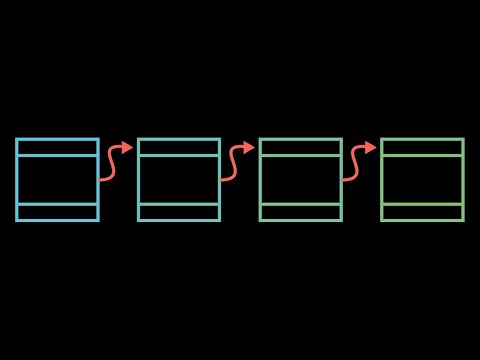 But how does bitcoin actually work?
How does bitcoin work? What is a "block chain"? What problem is this system trying to solve, and how does it use the tools of cryptography to do so?
Jul 7, 2017
But how does bitcoin actually work?
How does bitcoin work? What is a "block chain"? What problem is this system trying to solve, and how does it use the tools of cryptography to do so?
Jul 7, 2017
 How secure is 256 bit security?
When a piece of cryptography is described as having "256-bit security", what exactly does that mean? Just how big is the number 2^256?
Jul 8, 2017
How secure is 256 bit security?
When a piece of cryptography is described as having "256-bit security", what exactly does that mean? Just how big is the number 2^256?
Jul 8, 2017
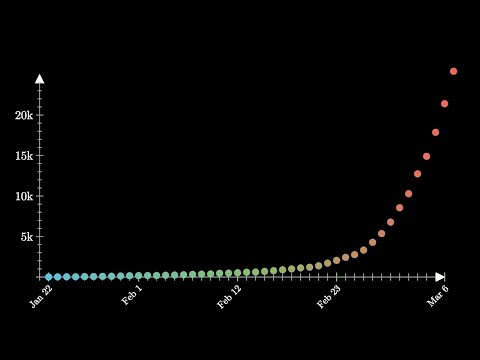 Exponential growth and epidemics
A primer on exponential and logistic growth, with epidemics as a central example
Mar 8, 2020
Exponential growth and epidemics
A primer on exponential and logistic growth, with epidemics as a central example
Mar 8, 2020
 Simulating an epidemic
SIR models for epidemics, showing how tweakign behavior can change an outbreak.
Mar 27, 2020
Simulating an epidemic
SIR models for epidemics, showing how tweakign behavior can change an outbreak.
Mar 27, 2020
 The DP-3T algorithm for contact tracing (via Nicky Case)
An overview of a simplified version of the DP-3T algorithm for privacy-first contact-tracing
May 14, 2020
The DP-3T algorithm for contact tracing (via Nicky Case)
An overview of a simplified version of the DP-3T algorithm for privacy-first contact-tracing
May 14, 2020
 Group theory, abstraction, and the 196,883-dimensional monster
An introduction to group theory, and the monster group.
Aug 19, 2020
Group theory, abstraction, and the 196,883-dimensional monster
An introduction to group theory, and the monster group.
Aug 19, 2020
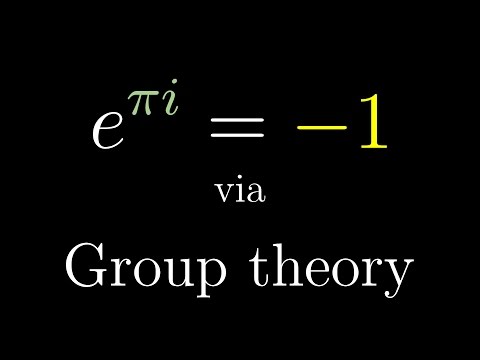 Euler's formula with introductory group theory
Euler's formula, e^{pi i} = -1, is one of the most famous expressions in math, but why on earth is this true? A few perspectives from the field of group theory can make this formula a bit more intuitive.
Mar 3, 2017
Euler's formula with introductory group theory
Euler's formula, e^{pi i} = -1, is one of the most famous expressions in math, but why on earth is this true? A few perspectives from the field of group theory can make this formula a bit more intuitive.
Mar 3, 2017
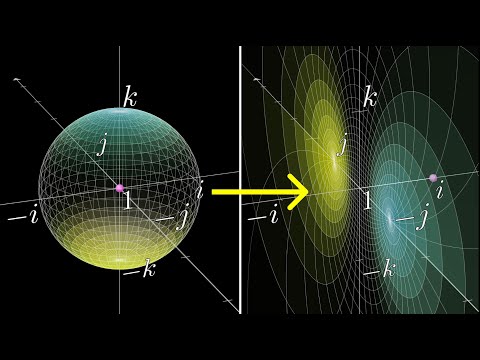 Visualizing quaternions (4d numbers) with stereographic projection
How to visualize quaternions, a 4d number system, in our 3d world
Sep 6, 2018
Visualizing quaternions (4d numbers) with stereographic projection
How to visualize quaternions, a 4d number system, in our 3d world
Sep 6, 2018
 Quaternions and 3d rotation, explained interactively
An introduction to an interactive experience on why quaternions describe 3d rotations
Oct 26, 2018
Quaternions and 3d rotation, explained interactively
An introduction to an interactive experience on why quaternions describe 3d rotations
Oct 26, 2018
 Thinking outside the 10-dimensional box
A method for thinking about high-dimensional spheres, introduced in the context of a classic example involving a high-dimensional sphere inside a high-dimensional box.
Aug 11, 2017
Thinking outside the 10-dimensional box
A method for thinking about high-dimensional spheres, introduced in the context of a classic example involving a high-dimensional sphere inside a high-dimensional box.
Aug 11, 2017
 Lockdown math announcement
Apr 16, 2020
Lockdown math announcement
Apr 16, 2020
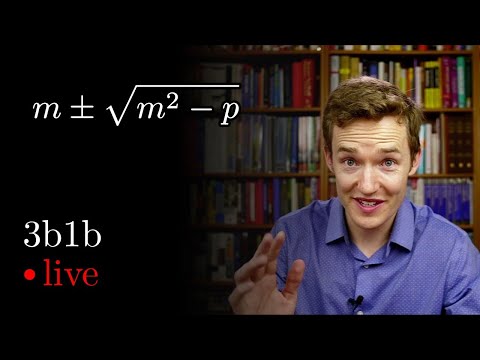 The simpler quadratic formula | Lockdown math ep. 1
Apr 17, 2020
The simpler quadratic formula | Lockdown math ep. 1
Apr 17, 2020
 Trigonometry fundamentals | Lockdown math ep. 2
Apr 21, 2020
Trigonometry fundamentals | Lockdown math ep. 2
Apr 21, 2020
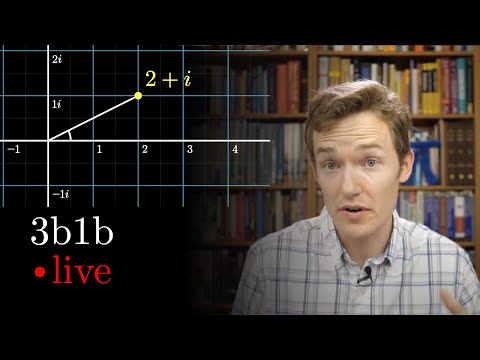 Complex number fundamentals | Lockdown math ep. 3
Apr 24, 2020
Complex number fundamentals | Lockdown math ep. 3
Apr 24, 2020
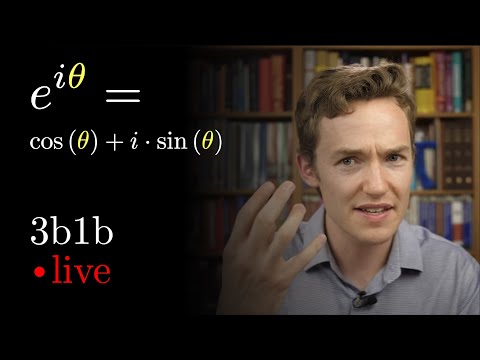 What is Euler's formula actually saying? | Lockdown math ep. 4
Apr 28, 2020
What is Euler's formula actually saying? | Lockdown math ep. 4
Apr 28, 2020
 Imaginary interest rates | Lockdown math ep. 5
May 1, 2020
Imaginary interest rates | Lockdown math ep. 5
May 1, 2020
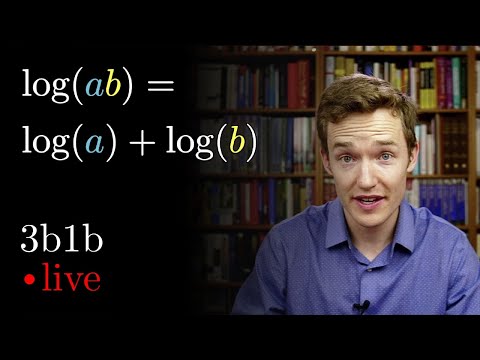 Logarithm Fundamentals | Lockdown math ep. 6
May 5, 2020
Logarithm Fundamentals | Lockdown math ep. 6
May 5, 2020
 What makes the natural log "natural"? | Lockdown math ep. 7
May 8, 2020
What makes the natural log "natural"? | Lockdown math ep. 7
May 8, 2020
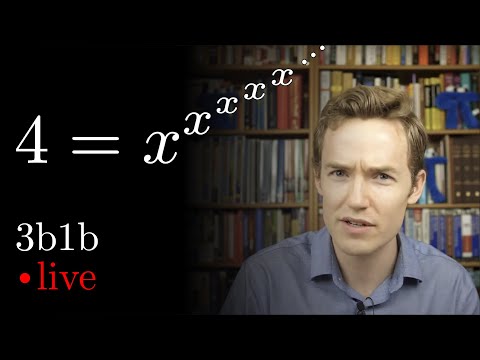 The power tower puzzle | Lockdown math ep. 8
May 12, 2020
The power tower puzzle | Lockdown math ep. 8
May 12, 2020
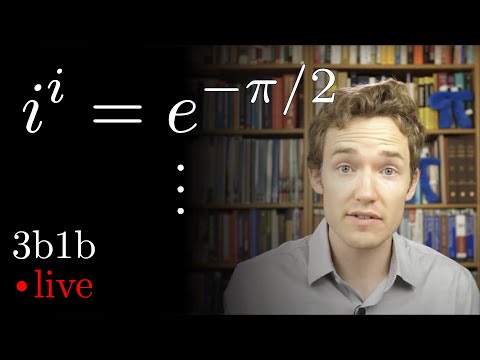 Intuition for i to the power i | Lockdown math ep. 9
May 15, 2020
Intuition for i to the power i | Lockdown math ep. 9
May 15, 2020
 Tips to be a better problem solver [Last lecture] | Lockdown math ep. 10
May 22, 2020
Tips to be a better problem solver [Last lecture] | Lockdown math ep. 10
May 22, 2020
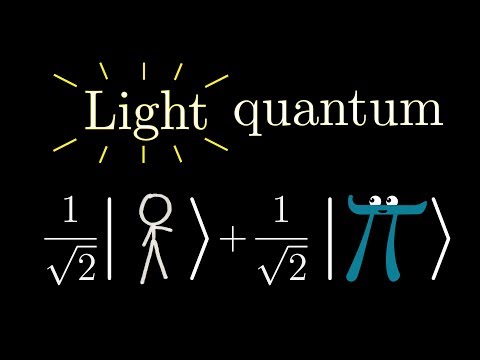 Some light quantum mechanics (with minutephysics)
An introduction to the quantum behavior of light, specifically the polarization of light. The emphasis is on how many ideas that seem "quantumly weird" are actually just wave mechanics, applicable in a lot of classical physics.
Sep 13, 2017
Some light quantum mechanics (with minutephysics)
An introduction to the quantum behavior of light, specifically the polarization of light. The emphasis is on how many ideas that seem "quantumly weird" are actually just wave mechanics, applicable in a lot of classical physics.
Sep 13, 2017
 Feynman's Lost Lecture (ft. 3Blue1Brown)
This video recounts a lecture by Richard Feynman giving an elementary demonstration of why planets orbit in ellipses. See the excellent book by Judith and David Goodstein, "Feynman's lost lecture”, for the full story behind this lecture, and a deeper dive into its content.
Jul 20, 2018
Feynman's Lost Lecture (ft. 3Blue1Brown)
This video recounts a lecture by Richard Feynman giving an elementary demonstration of why planets orbit in ellipses. See the excellent book by Judith and David Goodstein, "Feynman's lost lecture”, for the full story behind this lecture, and a deeper dive into its content.
Jul 20, 2018
 The Brachistochrone, with Steven Strogatz
A classic problem that Johann Bernoulli posed to famous mathematicians of his time, such as Newton, and how Bernoulli found an incredibly clever solution using properties of light.
Apr 1, 2016
The Brachistochrone, with Steven Strogatz
A classic problem that Johann Bernoulli posed to famous mathematicians of his time, such as Newton, and how Bernoulli found an incredibly clever solution using properties of light.
Apr 1, 2016
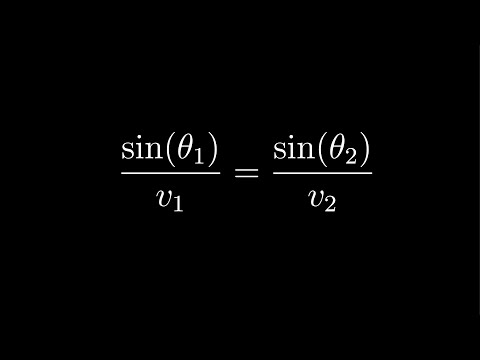 Snell's law proof using springs
A clever mechanical proof of Snell's law.
Apr 1, 2016
Snell's law proof using springs
A clever mechanical proof of Snell's law.
Apr 1, 2016
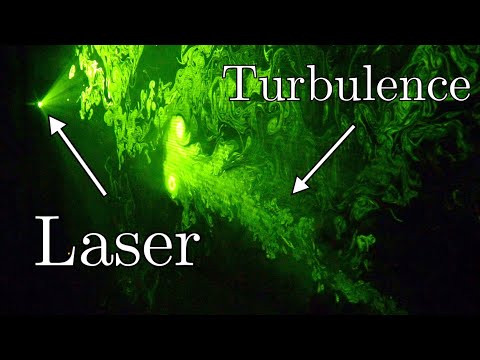 Why 5/3 is a fundamental constant for turbulence
A look at what turbulence is (in fluid flow), and a result by Kolmogorov regarding the energy cascade of turbulence.
Nov 7, 2018
Why 5/3 is a fundamental constant for turbulence
A look at what turbulence is (in fluid flow), and a result by Kolmogorov regarding the energy cascade of turbulence.
Nov 7, 2018
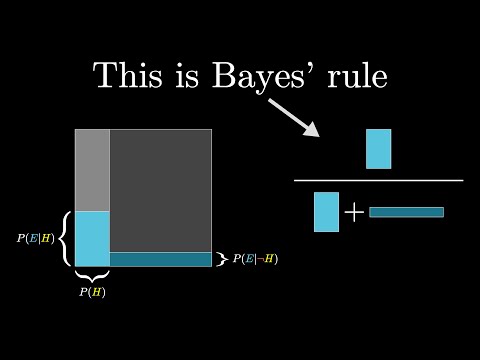 Bayes theorem
A visual way to think about Bayes' theorem, together with discussion on what makes the laws of probability more intuitive.
Dec 22, 2019
Bayes theorem
A visual way to think about Bayes' theorem, together with discussion on what makes the laws of probability more intuitive.
Dec 22, 2019
 The medical test paradox: Can redesigning Bayes rule help?
Dec 22, 2020
The medical test paradox: Can redesigning Bayes rule help?
Dec 22, 2020
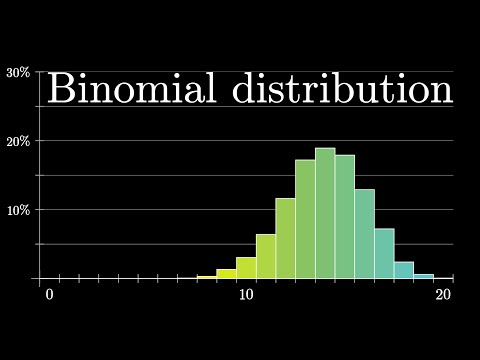 Binomial distributions | Probabilities of probabilities, part 1
The binomial distribution, introduced as setup to talk about the beta distribution
Mar 15, 2020
Binomial distributions | Probabilities of probabilities, part 1
The binomial distribution, introduced as setup to talk about the beta distribution
Mar 15, 2020
 Why “probability of 0” does not mean “impossible” | Probabilities of probabilities, part 2
Introduction to probability density functions.
Apr 12, 2020
Why “probability of 0” does not mean “impossible” | Probabilities of probabilities, part 2
Introduction to probability density functions.
Apr 12, 2020
 Q&A with Grant Sanderson (3blue1brown)
A simple Q&A
Aug 24, 2018
Q&A with Grant Sanderson (3blue1brown)
A simple Q&A
Aug 24, 2018
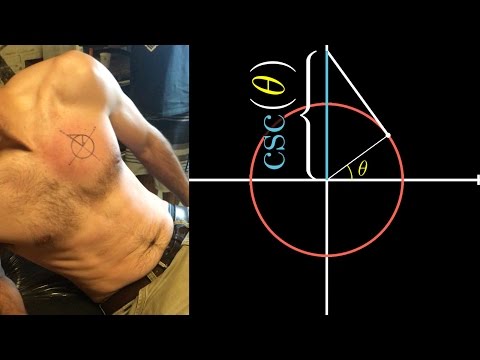 Tattoos on Math
After a friend of mine got a tattoo with a representation of the cosecant function, it got me thinking about how there's another sense in which this function is a tattoo on math, so to speak.
Jan 6, 2017
Tattoos on Math
After a friend of mine got a tattoo with a representation of the cosecant function, it got me thinking about how there's another sense in which this function is a tattoo on math, so to speak.
Jan 6, 2017
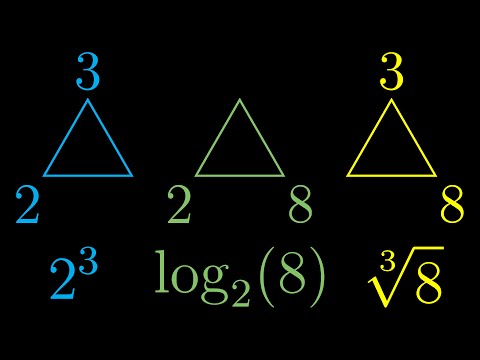 Triangle of Power
Logarithms are confusing, but perhaps some alternate notation could make them more intuitive.
Jun 26, 2016
Triangle of Power
Logarithms are confusing, but perhaps some alternate notation could make them more intuitive.
Jun 26, 2016
 How to count to 1000 on two hands
How to count in binary, and how this lets you count to 1023 on two hands.
Sep 18, 2015
How to count to 1000 on two hands
How to count in binary, and how this lets you count to 1023 on two hands.
Sep 18, 2015
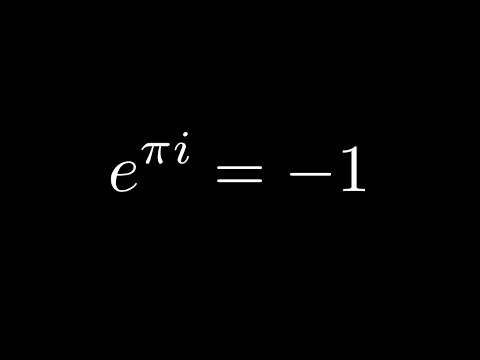 e to the pi i, a nontraditional take (old version)
The enigmatic equation e^{pi i} = -1 is usually explained using Taylor's formula during a calculus class. This video offers a different perspective, which involves thinking about numbers as actions, and about e^x as something which turns one action into another.
Mar 5, 2015
e to the pi i, a nontraditional take (old version)
The enigmatic equation e^{pi i} = -1 is usually explained using Taylor's formula during a calculus class. This video offers a different perspective, which involves thinking about numbers as actions, and about e^x as something which turns one action into another.
Mar 5, 2015
 Euler's Formula Poem
A silly poem encapsulating the ideas from the video about Euler's formula through graph theory.
Mar 5, 2015
Euler's Formula Poem
A silly poem encapsulating the ideas from the video about Euler's formula through graph theory.
Mar 5, 2015
 Blank Lesson
Brief, 1-2 sentence description of lesson. Shows under search results and elsewhere.
Dec 24, 2112
Blank Lesson
Brief, 1-2 sentence description of lesson. Shows under search results and elsewhere.
Dec 24, 2112
 Testbed Lesson
Brief, 1-2 sentence description of lesson. Shows under search results and elsewhere.
Dec 24, 2112
Testbed Lesson
Brief, 1-2 sentence description of lesson. Shows under search results and elsewhere.
Dec 24, 2112
 A quick trick for computing eigenvalues
A quick way to compute eigenvalues of a 2x2 matrix
May 7, 2021
A quick trick for computing eigenvalues
A quick way to compute eigenvalues of a 2x2 matrix
May 7, 2021
 How (and why) to raise e to the power of a matrix | DE6
Exponentiating matrices, and the kinds of linear differential equations this solves.
Apr 1, 2021
How (and why) to raise e to the power of a matrix | DE6
Exponentiating matrices, and the kinds of linear differential equations this solves.
Apr 1, 2021
 The medical test paradox: Can redesigning Bayes rule help?
Dec 22, 2020
The medical test paradox: Can redesigning Bayes rule help?
Dec 22, 2020
 Hamming codes and error correction
A discovery-oriented introduction to error correction codes.
Sep 4, 2020
Hamming codes and error correction
A discovery-oriented introduction to error correction codes.
Sep 4, 2020
 Hamming codes part 2, the elegance of it all
How to implement Hamming Codes with xors
Sep 4, 2020
Hamming codes part 2, the elegance of it all
How to implement Hamming Codes with xors
Sep 4, 2020
 Group theory, abstraction, and the 196,883-dimensional monster
An introduction to group theory, and the monster group.
Aug 19, 2020
Group theory, abstraction, and the 196,883-dimensional monster
An introduction to group theory, and the monster group.
Aug 19, 2020
 The impossible chessboard puzzle
An information puzzle with an interesting twist
Jul 5, 2020
The impossible chessboard puzzle
An information puzzle with an interesting twist
Jul 5, 2020
 Tips to be a better problem solver [Last lecture] | Lockdown math ep. 10
May 22, 2020
Tips to be a better problem solver [Last lecture] | Lockdown math ep. 10
May 22, 2020
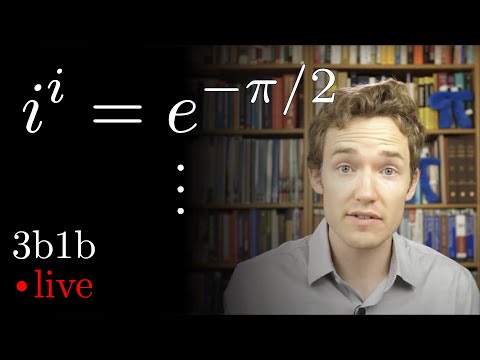 Intuition for i to the power i | Lockdown math ep. 9
May 15, 2020
Intuition for i to the power i | Lockdown math ep. 9
May 15, 2020
 The DP-3T algorithm for contact tracing (via Nicky Case)
An overview of a simplified version of the DP-3T algorithm for privacy-first contact-tracing
May 14, 2020
The DP-3T algorithm for contact tracing (via Nicky Case)
An overview of a simplified version of the DP-3T algorithm for privacy-first contact-tracing
May 14, 2020
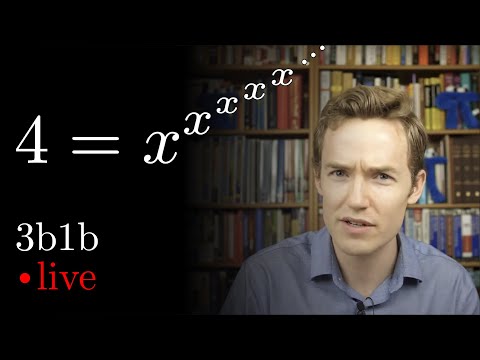 The power tower puzzle | Lockdown math ep. 8
May 12, 2020
The power tower puzzle | Lockdown math ep. 8
May 12, 2020
 What makes the natural log "natural"? | Lockdown math ep. 7
May 8, 2020
What makes the natural log "natural"? | Lockdown math ep. 7
May 8, 2020
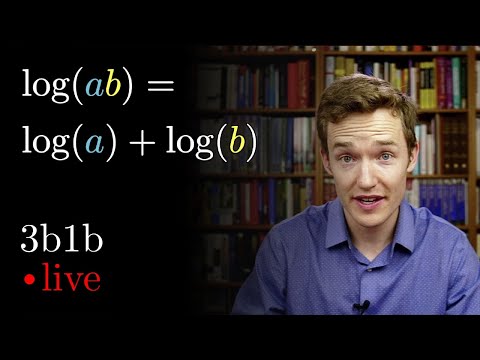 Logarithm Fundamentals | Lockdown math ep. 6
May 5, 2020
Logarithm Fundamentals | Lockdown math ep. 6
May 5, 2020
 Imaginary interest rates | Lockdown math ep. 5
May 1, 2020
Imaginary interest rates | Lockdown math ep. 5
May 1, 2020
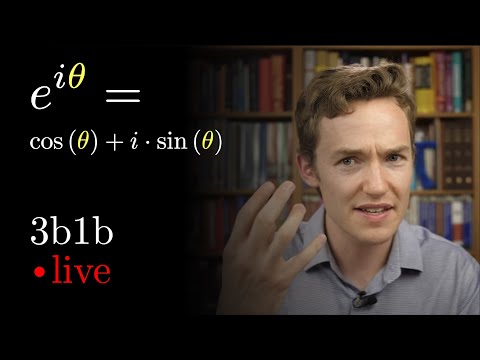 What is Euler's formula actually saying? | Lockdown math ep. 4
Apr 28, 2020
What is Euler's formula actually saying? | Lockdown math ep. 4
Apr 28, 2020
 Complex number fundamentals | Lockdown math ep. 3
Apr 24, 2020
Complex number fundamentals | Lockdown math ep. 3
Apr 24, 2020
 Trigonometry fundamentals | Lockdown math ep. 2
Apr 21, 2020
Trigonometry fundamentals | Lockdown math ep. 2
Apr 21, 2020
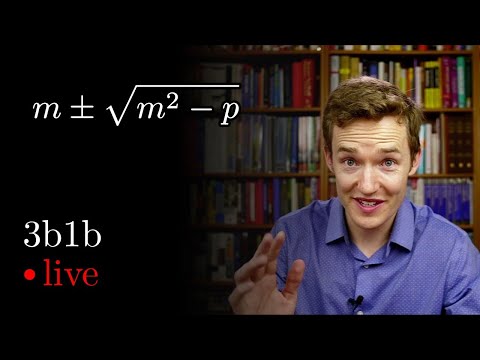 The simpler quadratic formula | Lockdown math ep. 1
Apr 17, 2020
The simpler quadratic formula | Lockdown math ep. 1
Apr 17, 2020
 Lockdown math announcement
Apr 16, 2020
Lockdown math announcement
Apr 16, 2020
 Why “probability of 0” does not mean “impossible” | Probabilities of probabilities, part 2
Introduction to probability density functions.
Apr 12, 2020
Why “probability of 0” does not mean “impossible” | Probabilities of probabilities, part 2
Introduction to probability density functions.
Apr 12, 2020
 Simulating an epidemic
SIR models for epidemics, showing how tweakign behavior can change an outbreak.
Mar 27, 2020
Simulating an epidemic
SIR models for epidemics, showing how tweakign behavior can change an outbreak.
Mar 27, 2020
 Binomial distributions | Probabilities of probabilities, part 1
The binomial distribution, introduced as setup to talk about the beta distribution
Mar 15, 2020
Binomial distributions | Probabilities of probabilities, part 1
The binomial distribution, introduced as setup to talk about the beta distribution
Mar 15, 2020
 Exponential growth and epidemics
A primer on exponential and logistic growth, with epidemics as a central example
Mar 8, 2020
Exponential growth and epidemics
A primer on exponential and logistic growth, with epidemics as a central example
Mar 8, 2020
 Bayes theorem
A visual way to think about Bayes' theorem, together with discussion on what makes the laws of probability more intuitive.
Dec 22, 2019
Bayes theorem
A visual way to think about Bayes' theorem, together with discussion on what makes the laws of probability more intuitive.
Dec 22, 2019
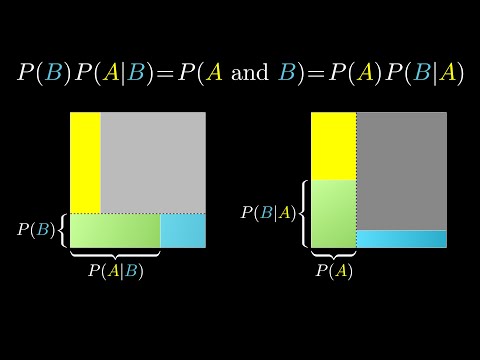 The quick proof of Bayes' theorem
A short explanation of why Bayes' theorem is true, together with discussion on a common misconception in probability
Dec 22, 2019
The quick proof of Bayes' theorem
A short explanation of why Bayes' theorem is true, together with discussion on a common misconception in probability
Dec 22, 2019
 Q&A with Grant (3blue1brown), windy walk edition
A simple Q&A
Nov 23, 2019
Q&A with Grant (3blue1brown), windy walk edition
A simple Q&A
Nov 23, 2019
 Why do prime numbers make these spirals?
A curious pattern in polar plots with prime numbers, together with discussion of Dirichlet's theorem
Oct 8, 2019
Why do prime numbers make these spirals?
A curious pattern in polar plots with prime numbers, together with discussion of Dirichlet's theorem
Oct 8, 2019
 The unexpectedly hard windmill question (2011 IMO, Q2)
Problem 2 from the 2011 IMO
Aug 4, 2019
The unexpectedly hard windmill question (2011 IMO, Q2)
Problem 2 from the 2011 IMO
Aug 4, 2019
 e^(iπ) in 3.14 minutes, using dynamics | DE5
A quick explanation of e^(pi i) in terms of motion and differential equations
Jul 7, 2019
e^(iπ) in 3.14 minutes, using dynamics | DE5
A quick explanation of e^(pi i) in terms of motion and differential equations
Jul 7, 2019
 Pure Fourier series animation montage
A montage of "fourier series" drawings, in which the sum of many rotated vectors traces an image
Jul 3, 2019
Pure Fourier series animation montage
A montage of "fourier series" drawings, in which the sum of many rotated vectors traces an image
Jul 3, 2019
 But what is a Fourier series? From heat flow to circle drawings | DE4
Fourier series, from the heat equation to sines to cycles.
Jun 30, 2019
But what is a Fourier series? From heat flow to circle drawings | DE4
Fourier series, from the heat equation to sines to cycles.
Jun 30, 2019
 Solving the heat equation | DE3
Solving the heat equation.
Jun 16, 2019
Solving the heat equation | DE3
Solving the heat equation.
Jun 16, 2019
 But what is a partial differential equation? | DE2
The heat equation, as an introductory PDE.
Apr 21, 2019
But what is a partial differential equation? | DE2
The heat equation, as an introductory PDE.
Apr 21, 2019
 Differential equations, studying the unsolvable | DE1
What is a differential equation, the pendulum equation, and some basic numerical methods
Mar 31, 2019
Differential equations, studying the unsolvable | DE1
What is a differential equation, the pendulum equation, and some basic numerical methods
Mar 31, 2019
 Cramer's rule, explained geometrically
What Cramer's rule is, and a geometric reason it's true
Mar 17, 2019
Cramer's rule, explained geometrically
What Cramer's rule is, and a geometric reason it's true
Mar 17, 2019
 How colliding blocks act like a beam of light...to compute pi.
The third and final part of the block collision sequence.
Feb 3, 2019
How colliding blocks act like a beam of light...to compute pi.
The third and final part of the block collision sequence.
Feb 3, 2019
 Why do colliding blocks compute pi?
A solution to the puzzle involving two blocks, sliding fricionlessly, where the number of collisions mysteriously computes pi
Jan 20, 2019
Why do colliding blocks compute pi?
A solution to the puzzle involving two blocks, sliding fricionlessly, where the number of collisions mysteriously computes pi
Jan 20, 2019
 The most unexpected answer to a counting puzzle
A puzzle involving colliding blocks where the number pi, vey unexpectedly, shows up.
Jan 13, 2019
The most unexpected answer to a counting puzzle
A puzzle involving colliding blocks where the number pi, vey unexpectedly, shows up.
Jan 13, 2019
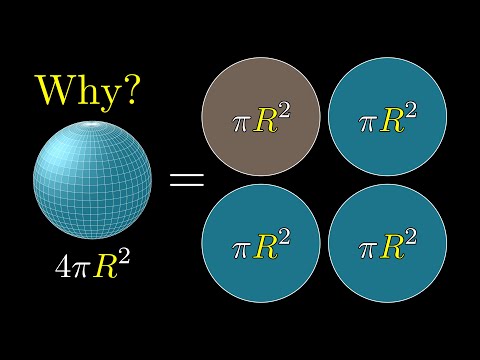 But why is a sphere's surface area four times its shadow?
Two proofs for the surface area of a sphere
Dec 2, 2018
But why is a sphere's surface area four times its shadow?
Two proofs for the surface area of a sphere
Dec 2, 2018
 Sneaky Topology | The Borsuk-Ulam theorem and stolen necklaces
Solving a discrete math puzzle, namely the stolen necklace problem, using topology, namely the Borsuk Ulam theorem
Nov 18, 2018
Sneaky Topology | The Borsuk-Ulam theorem and stolen necklaces
Solving a discrete math puzzle, namely the stolen necklace problem, using topology, namely the Borsuk Ulam theorem
Nov 18, 2018
 Why 5/3 is a fundamental constant for turbulence
A look at what turbulence is (in fluid flow), and a result by Kolmogorov regarding the energy cascade of turbulence.
Nov 7, 2018
Why 5/3 is a fundamental constant for turbulence
A look at what turbulence is (in fluid flow), and a result by Kolmogorov regarding the energy cascade of turbulence.
Nov 7, 2018
 Quaternions and 3d rotation, explained interactively
An introduction to an interactive experience on why quaternions describe 3d rotations
Oct 26, 2018
Quaternions and 3d rotation, explained interactively
An introduction to an interactive experience on why quaternions describe 3d rotations
Oct 26, 2018
 Visualizing quaternions (4d numbers) with stereographic projection
How to visualize quaternions, a 4d number system, in our 3d world
Sep 6, 2018
Visualizing quaternions (4d numbers) with stereographic projection
How to visualize quaternions, a 4d number system, in our 3d world
Sep 6, 2018
 Q&A with Grant Sanderson (3blue1brown)
A simple Q&A
Aug 24, 2018
Q&A with Grant Sanderson (3blue1brown)
A simple Q&A
Aug 24, 2018
 Why slicing a cone gives an ellipse
A beautiful proof of why slicing a cone gives an ellipse.
Aug 1, 2018
Why slicing a cone gives an ellipse
A beautiful proof of why slicing a cone gives an ellipse.
Aug 1, 2018
 Feynman's Lost Lecture (ft. 3Blue1Brown)
This video recounts a lecture by Richard Feynman giving an elementary demonstration of why planets orbit in ellipses. See the excellent book by Judith and David Goodstein, "Feynman's lost lecture”, for the full story behind this lecture, and a deeper dive into its content.
Jul 20, 2018
Feynman's Lost Lecture (ft. 3Blue1Brown)
This video recounts a lecture by Richard Feynman giving an elementary demonstration of why planets orbit in ellipses. See the excellent book by Judith and David Goodstein, "Feynman's lost lecture”, for the full story behind this lecture, and a deeper dive into its content.
Jul 20, 2018
 Divergence and curl: The language of Maxwell's equations, fluid flow, and more
Divergence, curl, and their relation to fluid flow and electromagnetism
Jun 21, 2018
Divergence and curl: The language of Maxwell's equations, fluid flow, and more
Divergence, curl, and their relation to fluid flow and electromagnetism
Jun 21, 2018
 The other way to visualize derivatives
A visual for derivatives which generalizes more nicely to topics beyond calculus. Thinking of a function as a transformation, the derivative measure how much that function locally stretches or squishes a given region.
May 19, 2018
The other way to visualize derivatives
A visual for derivatives which generalizes more nicely to topics beyond calculus. Thinking of a function as a transformation, the derivative measure how much that function locally stretches or squishes a given region.
May 19, 2018
 The Wallis product for pi, proved geometrically
A proof of the Wallis product for pi, together with some neat tricks using complex numbers to analyze circle geometry.
Apr 20, 2018
The Wallis product for pi, proved geometrically
A proof of the Wallis product for pi, together with some neat tricks using complex numbers to analyze circle geometry.
Apr 20, 2018
 Winding numbers and domain coloring
An algorithm for solving continuous 2d equations using winding numbers.
Mar 24, 2018
Winding numbers and domain coloring
An algorithm for solving continuous 2d equations using winding numbers.
Mar 24, 2018
 How pi was almost 6.283185...
A bit of the history behind how we came to use the symbol "pi" to represent what it does today, and how Euler used it to refer to several different circle constants.
Mar 14, 2018
How pi was almost 6.283185...
A bit of the history behind how we came to use the symbol "pi" to represent what it does today, and how Euler used it to refer to several different circle constants.
Mar 14, 2018
 Why is pi here? And why is it squared? A geometric answer to the Basel problem
A beautiful solution to the Basel Problem (1+1/4+1/9+1/16+...) using Euclidian geometry. Unlike many more common proofs, this one makes it very clear why pi is involved in the answer.
Mar 2, 2018
Why is pi here? And why is it squared? A geometric answer to the Basel problem
A beautiful solution to the Basel Problem (1+1/4+1/9+1/16+...) using Euclidian geometry. Unlike many more common proofs, this one makes it very clear why pi is involved in the answer.
Mar 2, 2018
 The more general uncertainty principle, beyond quantum
The general uncertainty principle, about the concentration of a wave vs the concentration of its fourier transform, applied to two non-quantum examples before showing what it means for the Heisenberg uncertainty principle.
Feb 25, 2018
The more general uncertainty principle, beyond quantum
The general uncertainty principle, about the concentration of a wave vs the concentration of its fourier transform, applied to two non-quantum examples before showing what it means for the Heisenberg uncertainty principle.
Feb 25, 2018
 But what is the Fourier Transform? A visual introduction.
An animated introduction to the Fourier Transform, winding graphs around circles.
Jan 26, 2018
But what is the Fourier Transform? A visual introduction.
An animated introduction to the Fourier Transform, winding graphs around circles.
Jan 26, 2018
 The three utilities puzzle with math/science YouTubers
A classic puzzle in graph theory, the "Utilities problem", a description of why it is unsolvable on a plane, and how it becomes solvable on surfaces with a different topology.
Dec 23, 2017
The three utilities puzzle with math/science YouTubers
A classic puzzle in graph theory, the "Utilities problem", a description of why it is unsolvable on a plane, and how it becomes solvable on surfaces with a different topology.
Dec 23, 2017
 The hardest problem on the hardest test
A geometry/probability question on the Putnam, a famously hard test, about a random tetrahedron in a sphere. This offers an opportunity not just for a lesson about the problem, but about problem-solving tactics in general.
Dec 8, 2017
The hardest problem on the hardest test
A geometry/probability question on the Putnam, a famously hard test, about a random tetrahedron in a sphere. This offers an opportunity not just for a lesson about the problem, but about problem-solving tactics in general.
Dec 8, 2017
 Backpropagation calculus
The math of backpropagation, the algorithm by which neural networks learn.
Nov 3, 2017
Backpropagation calculus
The math of backpropagation, the algorithm by which neural networks learn.
Nov 3, 2017
 What is backpropagation really doing?
An overview of backpropagation, the algorithm behind how neural networks learn.
Nov 3, 2017
What is backpropagation really doing?
An overview of backpropagation, the algorithm behind how neural networks learn.
Nov 3, 2017
 Gradient descent, how neural networks learn
An overview of gradient descent in the context of neural networks. This is a method used widely throughout machine learning for optimizing how a computer performs on certain tasks.
Oct 16, 2017
Gradient descent, how neural networks learn
An overview of gradient descent in the context of neural networks. This is a method used widely throughout machine learning for optimizing how a computer performs on certain tasks.
Oct 16, 2017
 But what is a Neural Network?
An overview of what a neural network is, introduced in the context of recognizing hand-written digits.
Oct 5, 2017
But what is a Neural Network?
An overview of what a neural network is, introduced in the context of recognizing hand-written digits.
Oct 5, 2017
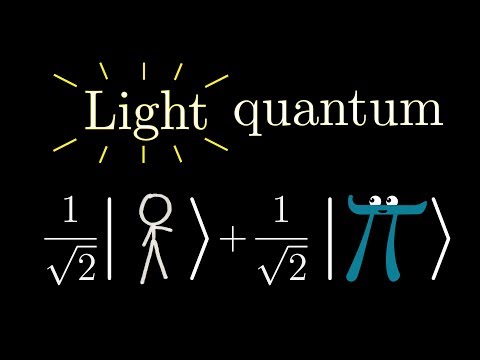 Some light quantum mechanics (with minutephysics)
An introduction to the quantum behavior of light, specifically the polarization of light. The emphasis is on how many ideas that seem "quantumly weird" are actually just wave mechanics, applicable in a lot of classical physics.
Sep 13, 2017
Some light quantum mechanics (with minutephysics)
An introduction to the quantum behavior of light, specifically the polarization of light. The emphasis is on how many ideas that seem "quantumly weird" are actually just wave mechanics, applicable in a lot of classical physics.
Sep 13, 2017
 Thinking outside the 10-dimensional box
A method for thinking about high-dimensional spheres, introduced in the context of a classic example involving a high-dimensional sphere inside a high-dimensional box.
Aug 11, 2017
Thinking outside the 10-dimensional box
A method for thinking about high-dimensional spheres, introduced in the context of a classic example involving a high-dimensional sphere inside a high-dimensional box.
Aug 11, 2017
 Hilbert's Curve: Is infinite math useful?
Drawing curves that fill all of space, and a philosophical take on why mathematics about infinite objects can still be useful in finite contexts.
Jul 21, 2017
Hilbert's Curve: Is infinite math useful?
Drawing curves that fill all of space, and a philosophical take on why mathematics about infinite objects can still be useful in finite contexts.
Jul 21, 2017
 How secure is 256 bit security?
When a piece of cryptography is described as having "256-bit security", what exactly does that mean? Just how big is the number 2^256?
Jul 8, 2017
How secure is 256 bit security?
When a piece of cryptography is described as having "256-bit security", what exactly does that mean? Just how big is the number 2^256?
Jul 8, 2017
 But how does bitcoin actually work?
How does bitcoin work? What is a "block chain"? What problem is this system trying to solve, and how does it use the tools of cryptography to do so?
Jul 7, 2017
But how does bitcoin actually work?
How does bitcoin work? What is a "block chain"? What problem is this system trying to solve, and how does it use the tools of cryptography to do so?
Jul 7, 2017
 All possible pythagorean triples, visualized
There are a few special right triangles many of us learn about in school, like the 3-4-5 triangle or the 5-12-13 triangle. Is there a way to understand all triplets of numbers (a, b, c) that satisfy a^2 + b^2 = c^2? There is! And it uses complex numbers in a clever way.
May 26, 2017
All possible pythagorean triples, visualized
There are a few special right triangles many of us learn about in school, like the 3-4-5 triangle or the 5-12-13 triangle. Is there a way to understand all triplets of numbers (a, b, c) that satisfy a^2 + b^2 = c^2? There is! And it uses complex numbers in a clever way.
May 26, 2017
 Pi hiding in prime regularities
A beutiful derivation of a formula for pi. At first, 1-1/3+1/5-1/7+1/9-.... seems unrelated to circles, but in fact there is a circle hiding here, as well as some interesting facts about prime numbers in the context of complex numbers.
May 19, 2017
Pi hiding in prime regularities
A beutiful derivation of a formula for pi. At first, 1-1/3+1/5-1/7+1/9-.... seems unrelated to circles, but in fact there is a circle hiding here, as well as some interesting facts about prime numbers in the context of complex numbers.
May 19, 2017
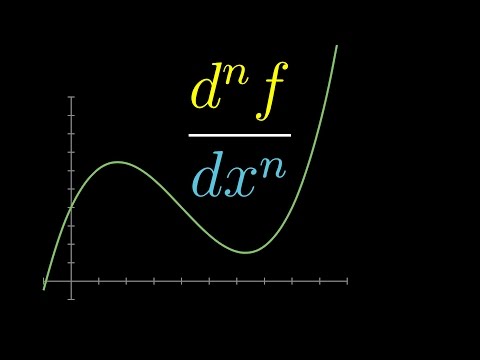 Higher order derivatives
What is the second derivative? Third derivative? How do you think about these?
May 7, 2017
Higher order derivatives
What is the second derivative? Third derivative? How do you think about these?
May 7, 2017
 Taylor series
Taylor series are extremely useful in engineering and math, but what are they? This video shows why they're useful, and how to make sense of the formula.
May 7, 2017
Taylor series
Taylor series are extremely useful in engineering and math, but what are they? This video shows why they're useful, and how to make sense of the formula.
May 7, 2017
 What does area have to do with slope?
Derivatives are about slope, and integration is about area. These ideas seem completely different, so why are they inverses?
May 6, 2017
What does area have to do with slope?
Derivatives are about slope, and integration is about area. These ideas seem completely different, so why are they inverses?
May 6, 2017
 Integration and the fundamental theorem of calculus
What is integration? Why is it computed as the opposite of differentiation? What is the fundamental theorem of calculus?
May 5, 2017
Integration and the fundamental theorem of calculus
What is integration? Why is it computed as the opposite of differentiation? What is the fundamental theorem of calculus?
May 5, 2017
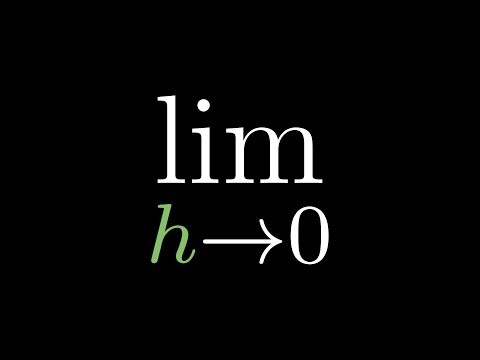 Limits, L'Hôpital's rule, and epsilon delta definitions
What are limits? How are they defined? How are they used to define the derivative? What is L'Hospital's rule?
May 4, 2017
Limits, L'Hôpital's rule, and epsilon delta definitions
What are limits? How are they defined? How are they used to define the derivative? What is L'Hospital's rule?
May 4, 2017
 Implicit differentiation, what's going on here?
How to think about implicit differentiation in terms of functions with multiple inputs, and tiny nudges to those inputs.
May 3, 2017
Implicit differentiation, what's going on here?
How to think about implicit differentiation in terms of functions with multiple inputs, and tiny nudges to those inputs.
May 3, 2017
 What's so special about Euler's number e?
What is the derivative of a^x? Why is e^x its own derivative? This video shows how to think about the rule for differentiating exponential functions.
May 2, 2017
What's so special about Euler's number e?
What is the derivative of a^x? Why is e^x its own derivative? This video shows how to think about the rule for differentiating exponential functions.
May 2, 2017
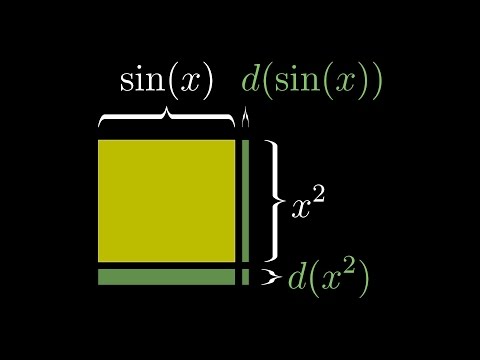 Visualizing the chain rule and product rule
The product rule and chain rule in calculus can feel like they were pulled out of thin air, but is there an intuitive way to think about them?
May 1, 2017
Visualizing the chain rule and product rule
The product rule and chain rule in calculus can feel like they were pulled out of thin air, but is there an intuitive way to think about them?
May 1, 2017
 Derivative formulas through geometry
Introduction to the derivatives of polynomial terms and trigonometric functions thought about geometrically and intuitively. The goal is for these formulas to feel like something the student could have discovered, rather than something to be memorized.
Apr 30, 2017
Derivative formulas through geometry
Introduction to the derivatives of polynomial terms and trigonometric functions thought about geometrically and intuitively. The goal is for these formulas to feel like something the student could have discovered, rather than something to be memorized.
Apr 30, 2017
 The paradox of the derivative
An introduction to what a derivative is, and how it formalizes an otherwise paradoxical idea.
Apr 29, 2017
The paradox of the derivative
An introduction to what a derivative is, and how it formalizes an otherwise paradoxical idea.
Apr 29, 2017
 The Essence of Calculus
An overview of what calculus is all about, with an emphasis on making it seem like something students could discover for themselves. The central example is that of rediscovering the formula for a circle's area, and how this is an isolated instance of the fundamental theorem of calculus
Apr 28, 2017
The Essence of Calculus
An overview of what calculus is all about, with an emphasis on making it seem like something students could discover for themselves. The central example is that of rediscovering the formula for a circle's area, and how this is an isolated instance of the fundamental theorem of calculus
Apr 28, 2017
 Euler's formula with introductory group theory
Euler's formula, e^{pi i} = -1, is one of the most famous expressions in math, but why on earth is this true? A few perspectives from the field of group theory can make this formula a bit more intuitive.
Mar 3, 2017
Euler's formula with introductory group theory
Euler's formula, e^{pi i} = -1, is one of the most famous expressions in math, but why on earth is this true? A few perspectives from the field of group theory can make this formula a bit more intuitive.
Mar 3, 2017
 Fractals are typically not self-similar
What exactly are fractals? A common misconception is that they are shapes which look exactly like themselves when you zoom in. In fact, the definition has something to do with the idea of "fractal dimension".
Jan 27, 2017
Fractals are typically not self-similar
What exactly are fractals? A common misconception is that they are shapes which look exactly like themselves when you zoom in. In fact, the definition has something to do with the idea of "fractal dimension".
Jan 27, 2017
 Tattoos on Math
After a friend of mine got a tattoo with a representation of the cosecant function, it got me thinking about how there's another sense in which this function is a tattoo on math, so to speak.
Jan 6, 2017
Tattoos on Math
After a friend of mine got a tattoo with a representation of the cosecant function, it got me thinking about how there's another sense in which this function is a tattoo on math, so to speak.
Jan 6, 2017
 Visualizing the Riemann zeta function and analytic continuation
What is the Riemann zeta function? What is analytic continuation? This video lays out the complex analysis needed to answer these questions.
Dec 9, 2016
Visualizing the Riemann zeta function and analytic continuation
What is the Riemann zeta function? What is analytic continuation? This video lays out the complex analysis needed to answer these questions.
Dec 9, 2016
 Binary, Hanoi and Sierpinski, part 1
How couting in binary can solve the famous tower's of hanoi problem.
Nov 25, 2016
Binary, Hanoi and Sierpinski, part 1
How couting in binary can solve the famous tower's of hanoi problem.
Nov 25, 2016
 Who cares about topology? (Inscribed rectangle problem)
This is an absolutely beautiful piece of math. It shows how certain ideas from topology, such as the mobius strip, can be used to solve a slightly softer form of an unsolved problem in geometry.
Nov 4, 2016
Who cares about topology? (Inscribed rectangle problem)
This is an absolutely beautiful piece of math. It shows how certain ideas from topology, such as the mobius strip, can be used to solve a slightly softer form of an unsolved problem in geometry.
Nov 4, 2016
 Abstract vector spaces
What is a vector space? Even though they are initial taught in the context of arrows in space, or with vectors being lists of numbers, the idea is much more general and far-reaching.
Sep 24, 2016
Abstract vector spaces
What is a vector space? Even though they are initial taught in the context of arrows in space, or with vectors being lists of numbers, the idea is much more general and far-reaching.
Sep 24, 2016
 Eigenvectors and eigenvalues
Eigenvalues and eigenvectors are one of the most important ideas in linear algebra, but what on earth are they?
Sep 15, 2016
Eigenvectors and eigenvalues
Eigenvalues and eigenvectors are one of the most important ideas in linear algebra, but what on earth are they?
Sep 15, 2016
 Change of basis
What is a change of basis, and how do you do it?
Sep 11, 2016
Change of basis
What is a change of basis, and how do you do it?
Sep 11, 2016
 Cross products
The cross product is a way to multiple to vectors in 3d. This video shows how to visualize what it means.
Sep 1, 2016
Cross products
The cross product is a way to multiple to vectors in 3d. This video shows how to visualize what it means.
Sep 1, 2016
 Cross products in the light of linear transformations
The formula for the cross product can feel like a mystery, or some kind of crazy coincidence. But it isn't. There is a fundamental connection between the cross product and determinants.
Sep 1, 2016
Cross products in the light of linear transformations
The formula for the cross product can feel like a mystery, or some kind of crazy coincidence. But it isn't. There is a fundamental connection between the cross product and determinants.
Sep 1, 2016
 Dot products and duality
What is the dot product? What does it represent? Why does it have the formula that it does? All this is explained visually.
Aug 24, 2016
Dot products and duality
What is the dot product? What does it represent? Why does it have the formula that it does? All this is explained visually.
Aug 24, 2016
 Nonsquare matrices as transformations between dimensions
How do you think about a non-square matrix as a transformation?
Aug 16, 2016
Nonsquare matrices as transformations between dimensions
How do you think about a non-square matrix as a transformation?
Aug 16, 2016
 Inverse matrices, column space and null space
How do you think about the column space and null space of a matrix visually? How do you think about the inverse of a matrix?
Aug 15, 2016
Inverse matrices, column space and null space
How do you think about the column space and null space of a matrix visually? How do you think about the inverse of a matrix?
Aug 15, 2016
 The determinant
The determinant has a very natural visual intuition, even though it's formula can make it seem more complicated than it really is.
Aug 10, 2016
The determinant
The determinant has a very natural visual intuition, even though it's formula can make it seem more complicated than it really is.
Aug 10, 2016
 Three-dimensional linear transformations
How to think of 3x3 matrices as transforming 3d space
Aug 9, 2016
Three-dimensional linear transformations
How to think of 3x3 matrices as transforming 3d space
Aug 9, 2016
 Matrix multiplication as composition
How to think about matrix multiplication visually as successively applying two different linear transformations.
Aug 8, 2016
Matrix multiplication as composition
How to think about matrix multiplication visually as successively applying two different linear transformations.
Aug 8, 2016
 Linear transformations and matrices
When you think of matrices as transforming space, rather than as grids of numbers, so much of linear algebra starts to make sense.
Aug 7, 2016
Linear transformations and matrices
When you think of matrices as transforming space, rather than as grids of numbers, so much of linear algebra starts to make sense.
Aug 7, 2016
 Linear combinations, span, and basis vectors
Some foundational ideas in linear algebra: Span, linear combinations, and linear dependence.
Aug 6, 2016
Linear combinations, span, and basis vectors
Some foundational ideas in linear algebra: Span, linear combinations, and linear dependence.
Aug 6, 2016
 Vectors, what even are they?
What is a vector? Is it an arrow in space? A list of numbers?
Aug 6, 2016
Vectors, what even are they?
What is a vector? Is it an arrow in space? A list of numbers?
Aug 6, 2016
 Essence of linear algebra preview
The introduction to a series on visualizing core ideas of linear algebra.
Aug 5, 2016
Essence of linear algebra preview
The introduction to a series on visualizing core ideas of linear algebra.
Aug 5, 2016
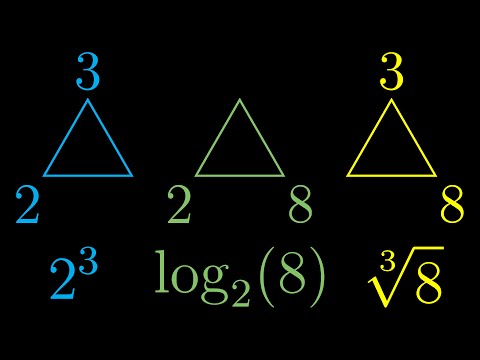 Triangle of Power
Logarithms are confusing, but perhaps some alternate notation could make them more intuitive.
Jun 26, 2016
Triangle of Power
Logarithms are confusing, but perhaps some alternate notation could make them more intuitive.
Jun 26, 2016
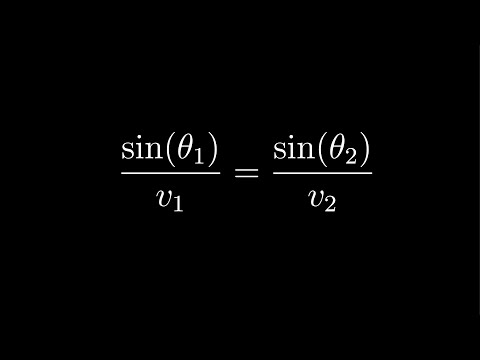 Snell's law proof using springs
A clever mechanical proof of Snell's law.
Apr 1, 2016
Snell's law proof using springs
A clever mechanical proof of Snell's law.
Apr 1, 2016
 The Brachistochrone, with Steven Strogatz
A classic problem that Johann Bernoulli posed to famous mathematicians of his time, such as Newton, and how Bernoulli found an incredibly clever solution using properties of light.
Apr 1, 2016
The Brachistochrone, with Steven Strogatz
A classic problem that Johann Bernoulli posed to famous mathematicians of his time, such as Newton, and how Bernoulli found an incredibly clever solution using properties of light.
Apr 1, 2016
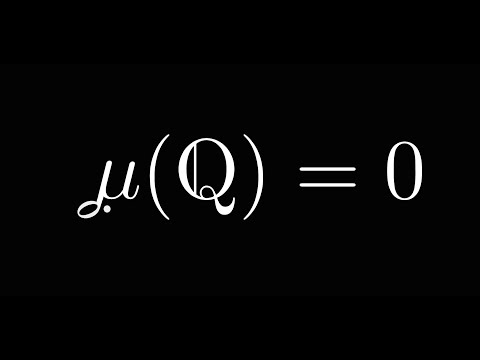 Music And Measure Theory
How one of the introductory ideas in a field called "measure theory" can be thought of in terms of musical harnomy and dissonance.
Oct 4, 2015
Music And Measure Theory
How one of the introductory ideas in a field called "measure theory" can be thought of in terms of musical harnomy and dissonance.
Oct 4, 2015
 How to count to 1000 on two hands
How to count in binary, and how this lets you count to 1023 on two hands.
Sep 18, 2015
How to count to 1000 on two hands
How to count in binary, and how this lets you count to 1023 on two hands.
Sep 18, 2015
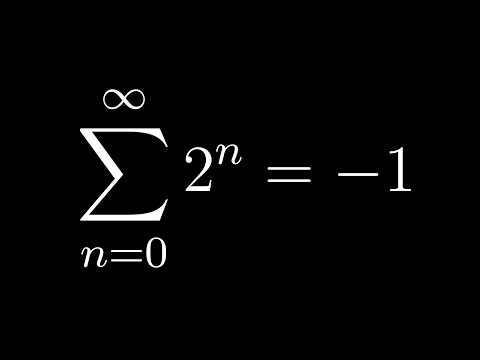 What does it feel like to invent math?
A journey through infinite sums, p-adic numbers, and what it feels like to invent new math.
Aug 14, 2015
What does it feel like to invent math?
A journey through infinite sums, p-adic numbers, and what it feels like to invent new math.
Aug 14, 2015
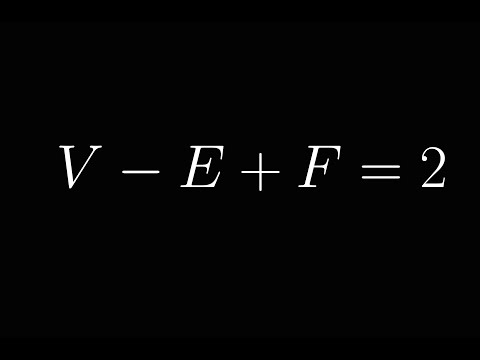 Euler's Formula and Graph Duality
A very clever proof of Euler's characteristic formula using spanning trees.
Jun 21, 2015
Euler's Formula and Graph Duality
A very clever proof of Euler's characteristic formula using spanning trees.
Jun 21, 2015
 Circle Division Solution
Moser's circle problem, and its solution.
May 24, 2015
Circle Division Solution
Moser's circle problem, and its solution.
May 24, 2015
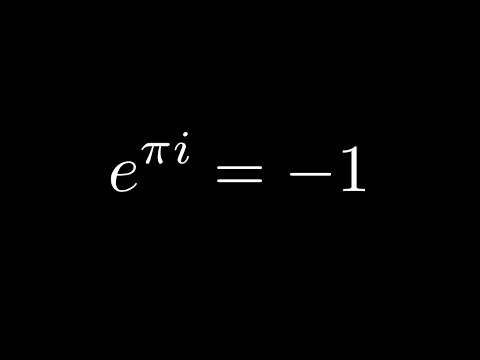 e to the pi i, a nontraditional take (old version)
The enigmatic equation e^{pi i} = -1 is usually explained using Taylor's formula during a calculus class. This video offers a different perspective, which involves thinking about numbers as actions, and about e^x as something which turns one action into another.
Mar 5, 2015
e to the pi i, a nontraditional take (old version)
The enigmatic equation e^{pi i} = -1 is usually explained using Taylor's formula during a calculus class. This video offers a different perspective, which involves thinking about numbers as actions, and about e^x as something which turns one action into another.
Mar 5, 2015
 Euler's Formula Poem
A silly poem encapsulating the ideas from the video about Euler's formula through graph theory.
Mar 5, 2015
Euler's Formula Poem
A silly poem encapsulating the ideas from the video about Euler's formula through graph theory.
Mar 5, 2015